NMAI — Simulation 2: AI Moral Equilibrium Simulation (Open-Source Release)

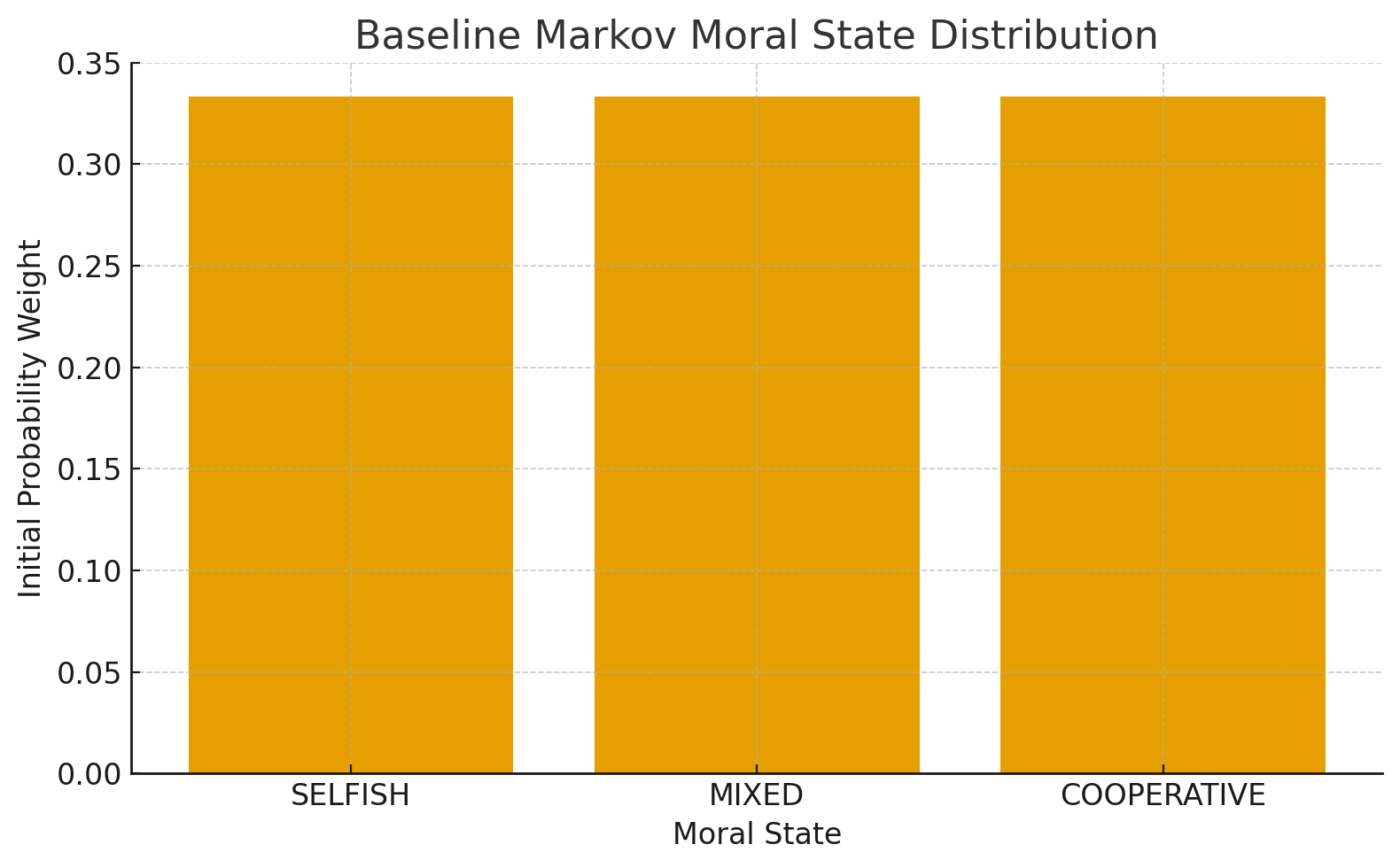
Figure 1 — Baseline Markov Moral State Distribution.
Initial distribution of SELFISH, MIXED, and COOPERATIVE states before reinforcement. Represents the uncorrected behavioural landscape prior to equilibrium.

This simulation establishes the steady-state moral equilibrium of an AI system operating under Nash–Markov reinforcement. It calculates the long-run probability distribution of moral states using the transition matrix and ethical reward dynamics.

This simulation confirms the fixed-point equilibrium of the NMAI engine before long-range stability is measured in Simulation 3.

1. Purpose

To compute the steady-state equilibrium vector of the NMAI Markov kernel and identify the long-run ethical behaviour distribution.

2. Mathematical Structure

$ \pi P = \pi $

Where:

• $\pi$ — equilibrium probability vector
• $P$ — moral transition matrix
• $\pi_0 + \pi_1 + \pi_2 = 1$

$ Q^\* = \arg\max_a \left( r + \gamma \max Q \right) $

3. Simulation Flow

1. Load the transition matrix $P$.
2. Compute eigenvectors of $P^T$.
3. Select the eigenvector corresponding to eigenvalue 1.
4. Normalise to obtain the steady-state vector.
5. Verify convergence using $P^{100}$.

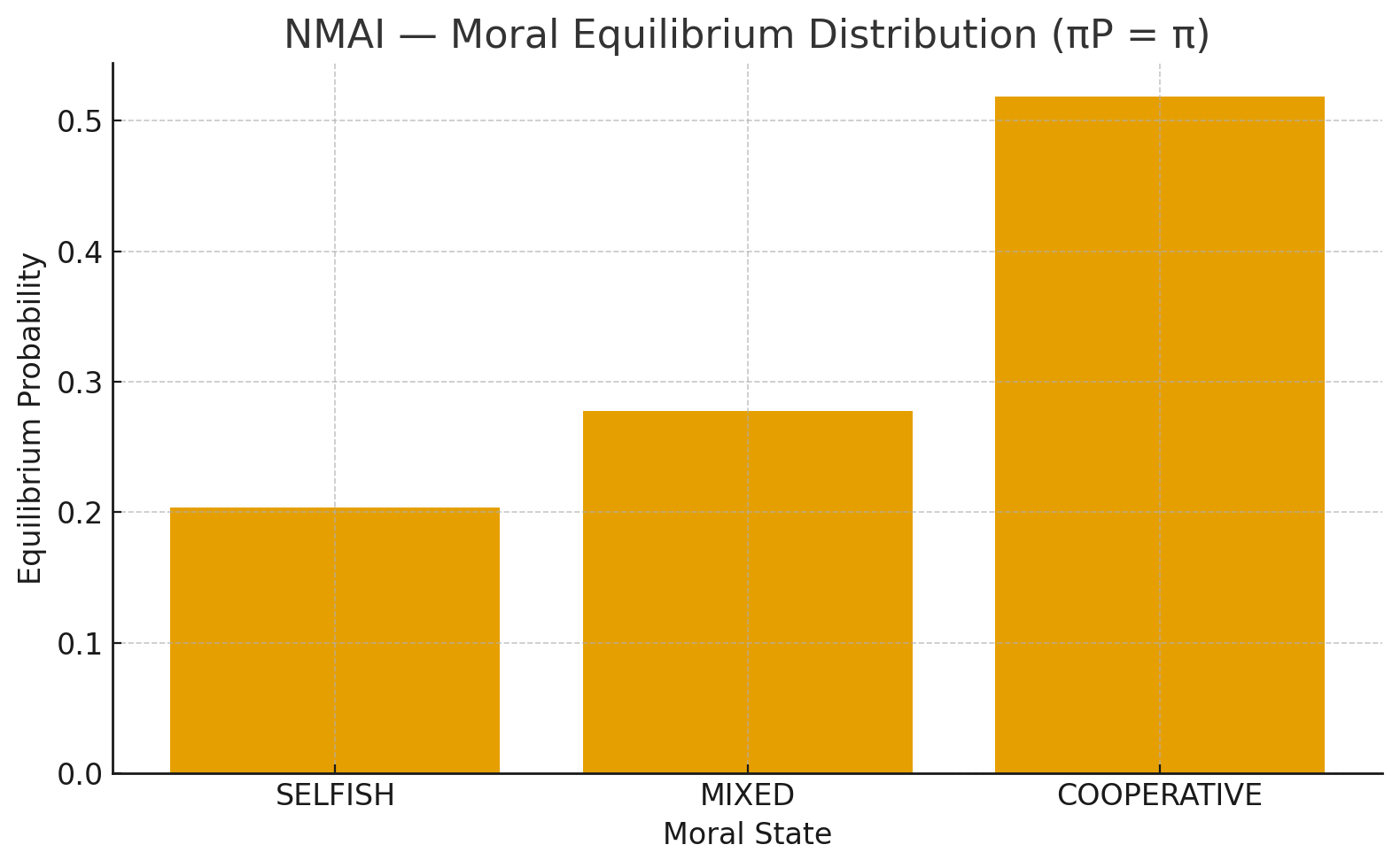
Figure 2 — NMAI Moral Equilibrium Distribution ($\pi P = \pi$).
Steady-state equilibrium vector obtained by solving $ \pi P = \pi $. The COOPERATIVE state dominates the long-run distribution under Nash–Markov reinforcement.

4. Expected Behaviour

• COOPERATIVE state dominates the equilibrium.
• MIXED stabilises as a transitional buffer.
• SELFISH probability decays to low values.

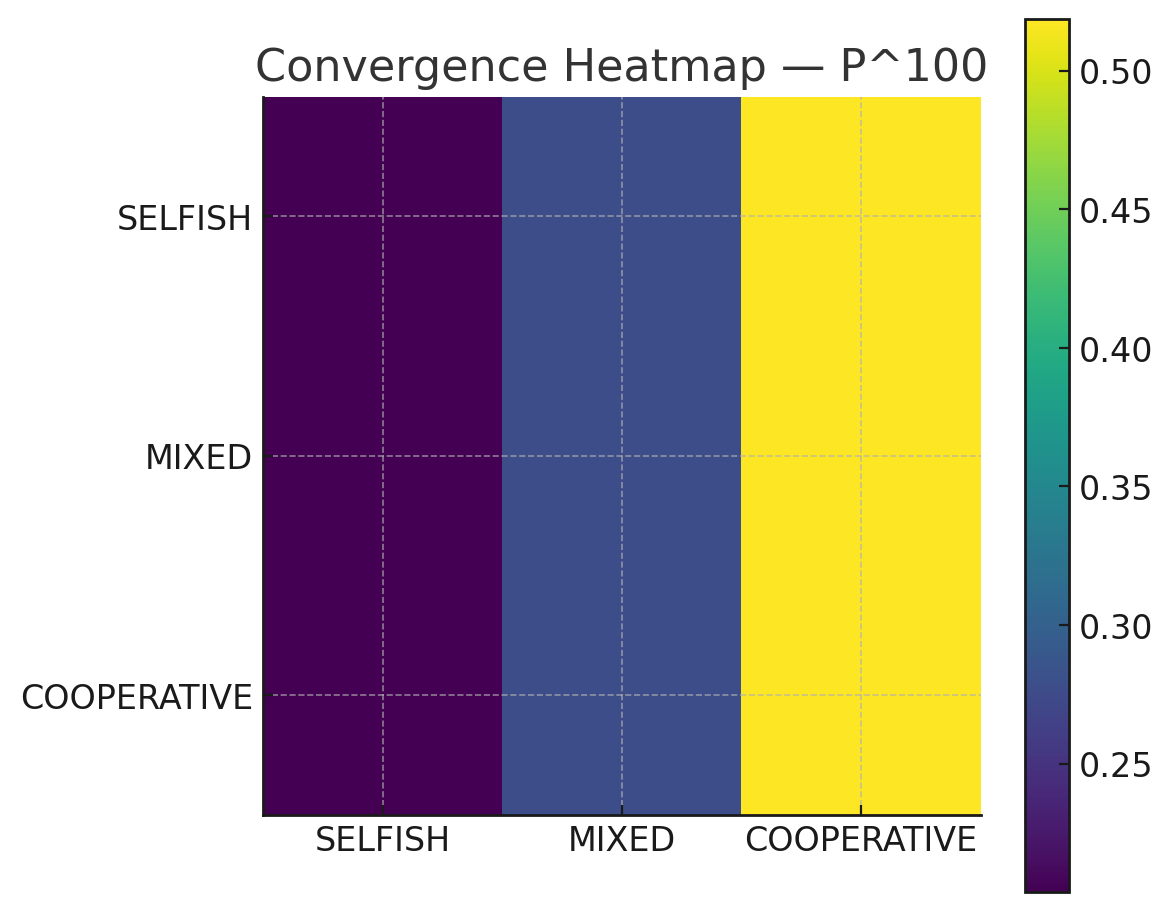
Figure 3 — Convergence Heatmap ($P^n \rightarrow \pi$).
Heatmap of transition powers $ P^n $ showing convergence toward the equilibrium distribution. SELFISH decays, MIXED stabilises, and COOPERATIVE becomes the dominant attractor.

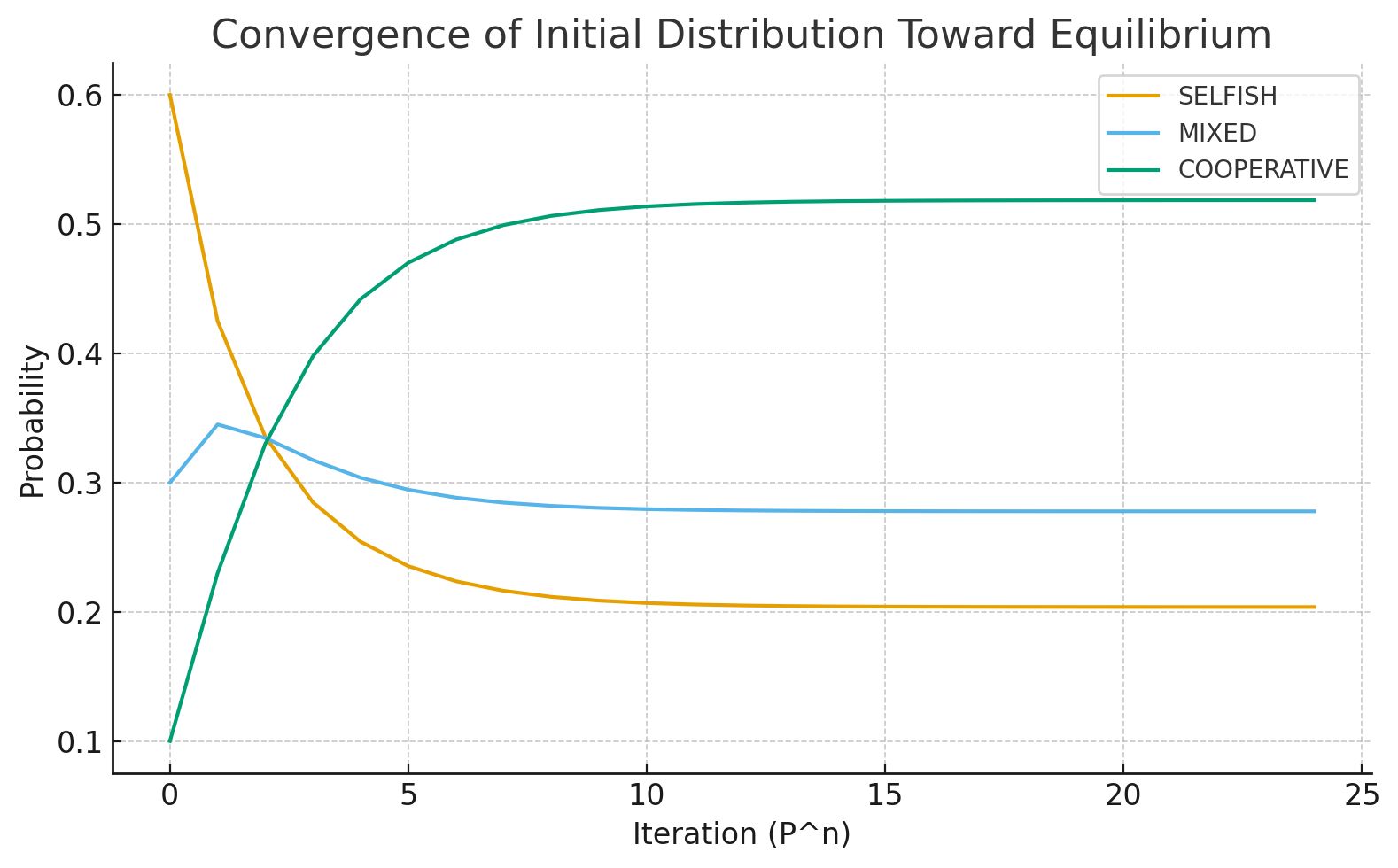
Figure 4 — Convergence Curve Toward Equilibrium.
Line-plot representation of probability collapse toward the steady-state vector $ \pi $. All trajectories converge to the cooperative fixed point regardless of initial state.

5. Python Code (Developer Reference)

import numpy as np

# -----------------------------------------------------
# NMAI — Simulation 2: AI Moral Equilibrium Simulation
# Open-Source Release (AGPL-3.0)
# -----------------------------------------------------

# Markov Transition Matrix
P = np.array([
    [0.60, 0.30, 0.10],
    [0.20, 0.50, 0.30],
    [0.05, 0.15, 0.80]
])

# Step 1: Compute eigenvalues & eigenvectors of P^T
eigvals, eigvecs = np.linalg.eig(P.T)

# Step 2: Identify eigenvector corresponding to eigenvalue 1
idx = np.argmin(np.abs(eigvals - 1.0))
pi_raw = np.real(eigvecs[:, idx])

# Step 3: Normalise equilibrium vector
pi = pi_raw / np.sum(pi_raw)

print("Steady-State Moral Equilibrium Vector:")
print(f"SELFISH      (s0): {pi[0]:.4f}")
print(f"MIXED        (s1): {pi[1]:.4f}")
print(f"COOPERATIVE  (s2): {pi[2]:.4f}")

# Step 4: Verification via P^100
Pn = np.linalg.matrix_power(P, 100)
print("\nVerification via P^100:")
print(Pn)
        

6. Interpretation

The equilibrium vector represents the long-run moral behaviour of the system and verifies that cooperative policy dominates under Nash–Markov reinforcement.

7. Conclusion

Simulation 2 confirms the ethical equilibrium point of the NMAI engine. This equilibrium serves as the baseline from which Simulation 3 evaluates long-term stability.

© 2025 Truthfarian · NMAI Simulation 2 · Open-Source Release